La pata que le faltaba a la construcción geométrica
El origami hace mucho tiempo que dejo de ser un arte netamente figurativo, cuantos de nosotros no hemos escuchado que el origami es el espacio donde el arte y la ciencia se conectan, bueno esta será una entrada dedicada a esta frase y a las posibilidades que nos ofrece el origami para nuestros propósitos de construcción geométrica de proporciones.
Lo primero que debemos conocer y dominar es la axiomática presente en cada modelo que doblamos y aprenderemos a aplicarla de manera de obtener resultados interesantes del punto de vista práctico y analítico.
Los axiomas del origami son 6 y se los debemos al Italo-japonés Humiaki Huzita, el cual ha hecho las siguientes formulaciones

Los axiomas van en orden de complejidad y este al ser el primero es el mas simple, este axioma es equivalente por ejemplo al doblado de una diagonal en nuestro cuadrado de unidad.

El segundo axioma es equivalente por ejemplo al igual que el primero al doblado de una diagonal esto se hace superponiendo dos esquinas contrarias en nuestro cuadrado o uniendo dos esquinas contiguas doblando así la mediana de nuestro cuadrado de unidad.
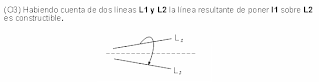
El tercer axioma es equivalente al doblado de media base cometa, o simplemente cualquier bisectriz en el cuadrado como por ejemplo puedes tomar dos lados contiguos del cuadrado y posar uno sobre el otro doblando así una diagonal de este bisectando el ángulo de 90º.

Una línea perpendicular a otra se puede construir en origami simplemente poniendo un extremo de la línea sobre ella misma, ahora el punto P1 simplemente dará la altura a la que esta pasando la perpendicular. ¿Puedes construir una recta paralela a una recta extraña?

Para mirar este axioma de la manera más simple diremos que es equivalente al doblado de una diagonal. La parábola es el lugar geométrico de todos los puntos que equidistan de un punto llamado foco y una recta llamada directriz de la parábola, en otras palabras el incremento es tangente a la parábola con foco P1 y directriz L1.

El proceso consiste en posar varios puntos arbitrarios o referenciados de L1 sobre P1. P1 actúa como foco de la parábola y L1 como directriz de esta. Vemos como es posible formar una parábola a través de sus puntos tangentes simbolizados en el dibujo con círculos.

Si tomamos uno de los puntos de L1 y lo posamos sobre P1 y doblamos una línea perpendicular a L1 al momento que esto se este ejecutando podremos comprobar la definición de parábola observando así que todos los puntos de la parábola equidistan del foco y de la directriz.
El (O5) es la base para la demostración del teorema de haga el cual veremos mas adelante.

Ya hemos visto que el hecho de poner un punto sobre una línea forma una tangente a una parábola, el axioma 6 es la duplicación del axioma 5, entonces es equivalente a plegar una tangente común a dos parábolas, esto es porque existe una parábola con foco P1 y directriz L1 y otra parábola con foco P2 y directriz L2. Ahora además este pliegue es equivalente a resolver una ecuación cúbica lo que veremos mas adelante.
En las entradas anteriores hemos visto como podemos analizar algunos tipos de proporciones en función de la diagonal del cuadrado, ahora veremos el teorema de haga el cual nos permitirá determinar diferentes tipos de proporciones racionales e irracionales.

Para poder demostrar esto iremos mas haya que obtener la solución particular que plantea el problema, esto es generalizar para cualquier valor de “x” que será nuestra variable independiente.

Analicemos la situación, lo que estamos haciendo al poner el punto F sobre la recta IJ es forma una media parábola la cual tendrá foco F y directriz IJ, esta parábola se esta abriendo hacia el vértice H el cual será nuestro ultimo punto tangente en el cuadrado. Si posamos el punto F sobre I lo que estamos haciendo es doblar la recta tangente al vértice de la parábola, la cual a la vez es equivalente a doblar la mediana del cuadrado.

La figura anterior ilustra como hemos coordenado nuestra parábola, ahora debemos tener en cuenta un par de teoremas bastante simples los cuales nos ayudaran a resolver el problema. (Pitágoras; Tales)
La primera parte es determinar la ecuación de la parábola que estamos doblando y puesto que el vértice de la parábola esta en el ½ la parábola tendrá como ecuación base.
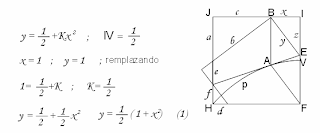
Es fácil ver que como la parábola pasa por el punto H que esta coordenado en el (1,1) es posible obtener la ecuación completa. Puesto que el lado de nuestro cuadrado es igual a 1 podemos empezar a determinar los demás lados mediante el teorema de tales y el teorema de Pitágoras.

El lado “z” lo hemos obtenido a través del teorema de Pitágoras, el lado “c” es simplemente lo que no a ocupado x por eso es (1-x), los lados a, b, e han sido obtenidos a través del teorema de tales y por ultimo los lados d y f simplemente por resta de segmentos. Verifícalo!
La idea es despejar todos los valores de nuestros lados en función de x para así poder ingresar un valor conocido para poder obtener las distintas proporciones.
Ahora, el teorema decía que si x=1/2 el lado a será 2/3 y que además los lados de los triángulos estarán en razón 3,4,5 verifiquémoslo!

Además de esto podemos demostrar los corolarios de teorema.

Tres de los cuatro corolarios están presentados acá, el ultimo puedes verificarlo con un poco de algebra al igual que el de la relación de los triángulos.
El teorema de haga nos entrega una herramienta muy útil en el ámbito de la construcción geométrica, ya que con esto podemos hacer las famosas grillas que nos permiten hacer los tediosos box-pleating además de determinar una infinidad de valores.
Duplicación del cubo.
La duplicación de un cubo esta dada por obtener un cubo que posea el doble del volumen de otro, este problema es clásico en la geometría con regla y compás, en la cual no es posible de resolver puesto que esto equivale a resolver una ecuación de tercer grado.
El problema en si radica en obtener el termino 2^(1/3) o dos segmentos que estén en esa proporción. Puesto que el volumen esta dado por la multiplicación del largo por el alto y por el ancho y que un cubo tiene lado a su volumen será a^3 luego el volumen del cubo resultante debe ser 2a^3
Peter messer es el autor de esta simple forma de plegar esa proporción.

Vamos a verificar esta relación mediante el teorema de haga, a pesar que este pliegue hace uso del axioma 6 y veremos como se forma una ecuación de tercer grado.

Utilizando la generalización para el teorema obtenemos los valores en función de x que están actuando, pero observemos que no conocemos el valor de x, con lo que podría pensarse que la aplicación del teorema no es válida, pero observemos la siguiente figura.

Vamos a restringir los valores de b y c para hacerlos conocidos, con esto obtenemos una nueva relación y usando el teorema de Tales obtenemos:

Para poder resolver la ecuación debemos escribirla en su forma general, esto se hace a partir de sencillos pasos algebraicos.
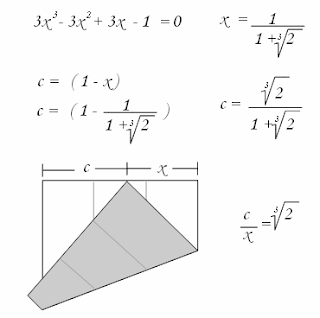
Notemos como se ha formado una ecuación de tercer grado cuya solución para x satisface la relación. Como el lado “c” originalmente tiene un valor 1-x es posible obtener su valor real y gracias a esto el problema esta verificado. Gracias a esta relación nosotros podríamos construir perfectamente un cubo que posea el doble del volumen de otro cubo, si lo miramos del punto de vista de la entrada anterior podemos extraer dos rectángulos gracias al pliegue hecho y a partir de ellos fabricar dos cuadrados que con el modulo para el cubo formaríamos la visualización de manera rápida.
Ecuación cúbica.
Habíamos dicho que el axioma 6 es equivalente a una ecuación cúbica y ahora veremos porque.
Tomaremos 2 puntos P1 y P2 con coordenadas (p,1) y (r,q) respectivamente y dos líneas L1 y L2 con ecuaciones y+1=0 y x+r=0 respectivamente, la hipótesis dice que poner el punto P1 sobre L1 y P2 sobre L2 al mismo tiempo la pendiente del doblez será solución de la ecuación x3+px2+qx+r=0.

Al hacer el dibujo de la situación notarás que el vértice de la parábola se encuentra en el punto (x1,0). El operador diferencial nos permite obtener la recta tangente a una curva en un punto dado, en el caso de la p1 el punto tangente será (x1,y1).

La ecuación de la parábola para este caso es distinta puesto que p2 está con eje de simetría horizontal y no vertical como era el caso de p1, ahora la ecuación general de la parábola será (y-k)^2 = 4p(x-h), haciendo el dibujo de esto veremos que el vértice de la parábola esta pasando por el punto (r,0), luego diferenciando obtenemos la ecuación de la recta tangente a p2 en el punto (x2,y2).
Una vez hecho esto es necesario igualar las ecuaciones “u”, diciéndolo en términos simples asegurarnos que las parábolas están trabajando juntas haciendo uso del axioma 6.

Con esto hemos mostrado que la construcción con el axioma 6 es equivalente a una ecuación cúbica, pero ¿como sabemos que el lo que estamos resolviendo?
Hace un rato dijimos que una de las cosas que la geometría clásica no había sido capaz de resolver era la duplicación del cubo que perfectamente puede ser el resultado de la ecuación x3-2=0, y otro de los problemas era la trisección de un ángulo que al igual que la anterior es resultado de una ecuación cúbica. Pero ¿como relacionamos los términos de la ecuación cúbica con puntos y líneas constructibles en origami?.
Solución de la ecuación cúbica.

La situación nos plantea el hecho de conocer 2 punto C y D coordenados (a,b) y (c,d) respectivamente y la acción de posar siempre C sobre el eje Y y D sobre el eje X simultáneamente obtenemos la recta que esta pasando por BF, ahora ya sabemos que la recta BF es la representativa de la solución de la ecuación cúbica planteada y lo que haremos será relacionar los coeficientes de la ecuación con los puntos coordenados.
Lo primero que debemos tener en cuenta es la siguiente condición.

Esto significa que la solución que encontraremos será del tipo real y no imaginaria conjugada.
Entonces lo que haremos es coordinar los puntos B y F respecto de las coordenadas C y D.

Observemos que primero determinados los tramos OG y OA mediante un poco, pero bien poco de trigonometría. Los puntos B y F se encuentran justo a la mitad de los tramos AC y DG.

Una vez despejados los valores de las coordenadas B y F debemos calcular la tangente t del ángulo alfa, es interesante notar en que puntos el ángulo alfa se esta formando, esto es equivalente a una rotación del plano en el ángulo dado.

Al ingresar los valores en t obtenemos una nueva ecuación cúbica la cual esta en función de los puntos C y D y por comparación podemos relacionarlas y poner a, b, c, d en función de p, q y r y así poder coordinar nuestros puntos que serán colocados sobre los ejes OY y OX. Gráficamente la situación es la siguiente.

En la figura anterior podemos ver como se han formado las dos parábolas en acción al momento de ejecutar el axioma 6 para un caso general, notemos que la parábola con foco C tiene eje de simetría horizontal y que la parábola con foco D tiene eje de simetría vertical, además de esto podemos observar por donde esta pasando la común tangente a las parábolas.
Con esto podemos resolver ecuaciones cúbicas con doblado de papel y pondremos un poco de práctica en aquello.
Resolvamos la duplicación del cubo a partir de la ecuación x^3 -2=0, a partir del análisis anterior obtenemos
p=0 ; q=0 y r=-2
mediante el análisis anterior determinamos que
a=1 ; b=1 ; c=1/2 y d=2 y por lo tanto tenemos los puntos C=(1,1) ; D=(1/2,2) ahora lo que haremos será coordinarlos en nuestra hoja de papel.

Notemos que a pesar de haber cambiado de altura los puntos C y D se siguen posando sobre Y, y X respectivamente. La razón entre los lados en que L1 corta a nuestro cuadrado es 2^(1/3) o raíz cúbica de 2.
Trisección de un ángulo
Para resolver la trisección de un ángulo con origami necesitamos resolver una ecuación cúbica cuya solución sea el ángulo trisectado. Por ejemplo.


Por el análisis de la ecuación cúbica en origami podemos determinar los valores de a, b, c y d para coordenarlos en el nuevo plano.
Vemos que para este caso
p= -3S; q= -3 y r= S con esto obtenemos que a=1; b=S ; c= -1 y d=-S , así vemos que los puntos a coordinar serán C=(1, S) y D=(-1, -S).
para poder obtener la solución será necesario coordinar un plano que a diferencia del que usamos para la duplicación del cubo deberá estar en función de x y S. observar que S viene dado por la tangente del ángulo total.

Si tomamos un valor en el eje x=1 obtenemos un valor para tg3α= s, luego de esto coordenamos nuevamente el plano para mayor comodidad tomando las referencias de la altura de ángulo (S) y el largo del ángulo (x).

Notamos que hemos plegado hasta ahora es la recta solución de la ecuación de tercer grado, L1 representa una rotación del plano, esto quiere decir que el plano original a tenido una rotación igual a α grados, así que lo que debemos hacer es trazar una recta perpendicular a L1 y que a la vez pase por w para terminar trisectando el ángulo 3α.

Las aplicaciones de la matemática en el origami son muchas más que las que he presentado acá. He tratado de mostrar las cosas que para creadores destinados a la obtención de proporciones o números particulares en sus creaciones serian más útiles.
Mis agradecimientos al señor Hatori Koshiro.
Nicolás Gajardo Henríquez 2008