Que pasa cuando nos enfrentamos a un modelo el cual tiene algunos requerimientos especiales más allá de la cantidad de puntas, si no que requiere cuidado en la distribución de estas. Si nos damos tiempo para pensar y revisar lo que tenemos hasta ahora (mirándolo desde el punto de vista de este Blog) nos damos cuenta que hemos utilizado solo bases conocidas y que las hemos hecho actuar de manera conjunta sin que nos preocupemos mas que por la cantidad de puntas que nos entregan y un poco de espacio entre ellas, ¿pero podemos manejar longitudes de una base que queramos construir?
Llamaremos puntos de salida a aquellos puntos en los cuales se esta liberando una aleta en nuestro papel.
Comenzaremos con un triangulo cualquiera, la manera de pegar esta figura es bastante simple y consiste en doblar sus bisectrices y sus puntos de salida están dados por la línea perpendicular a sus lados que sale desde el incentro.

En rigor no es la única forma de plegar un triangulo, pero si es la única forma de doblarlo y que quede plano o en otras palabras que sus segmentos liberados estén sobre un mismo eje y eso es lo que nos importa. El pliegue que hemos generado es conocido por todos y para el que no lo sepa por ponerle nombre algún sujeto lo nombró pliegue oreja de conejo. La secuencia y el triangulo mostrado son solo para hacer una generalidad, pero a partir de este pliegue podemos construir todas las bases tradicionales.
Si tomamos un cuadrado unidad y aplicamos el mismo sistema, ya sea dividiéndolo en triángulos o como cuadrilátero es posible aplanarlo sin problema, ahora ¿podemos manejar las longitudes de este cuadrado?
Hay que tener en claro que la acción de manejar las longitudes no generará segmentos totalmente independientes, esto significa que un segmento es la consecuencia de otro. Observemos la base pez y noten como he tomado sus líneas fundamentales y las he reducido de escala progresivamente hasta 0 y he logrado la base bomba de agua.

¿Interesante u obvio?
Si aislamos la figura es sencillo ver lo que pasa y como se comporta el punto de salida que sigue saliendo desde el incentro.

Lo que hemos hecho es solo una particularidad, pero nos permite hacernos una idea de cómo un segmento influye en el otro y a la vez darnos luces de los elementos necesarios para lograr una generalización, ahora hagamos lo mismo con la base pájaro.

Si tomamos un cuadrilátero cualquiera con bisectrices que llegan a un único punto en él entonces es posible ensamblarlo de la misma manera que la base bomba de agua.
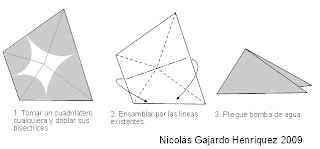
Observemos los siguientes diagramas de círculos para nuestro cuadrilátero, podemos ver como los círculos en el primero son tangentes entre ellos indicando así el radio de acción de cada punta, en la segunda figura vemos que los puntos tangentes a la circunferencia inscrita en el cuadrilátero son los mismo que delimitan el actuar de los segmentos.

Ahora veamos que dentro del mismo cuadrilátero podemos inscribir distintos tipos de diagramas de círculos tangentes entre si.

Elegiremos uno al azar y lo haremos cumplir con las condiciones dispuestas por los círculos

Vemos que la orientación que hemos elegido es completamente posible de doblar, y si bien es cierto que es un poco minucioso el doblado de esta, las ventajas en cuanto a distribución de segmentos son importantes. Es importante decir que esta no es la única manera de conseguir esta misma distribución, pero si la que personalmente me gusta. Ahora, si miramos el plano de la estructura que hemos generado observaremos que las longitudes de los segmentes son dirigidas desde las cúspides de los dos triángulos en el centro de la estructura y que en si esta funcionando de la misma manera que los sistemas en 22,5 grados descritos en las entradas anteriores con triángulos de compensación.
Continuara…
1 comentario:
Nicolás
Nuevamente una entrada muy interesante (esperando la continuación), me gusta mucho la explicación de estas moléculas tan famosas de una forma simple y muy comprensible.
Saludos,
Andrés
Publicar un comentario